Page 66 - Telebrasil - Março/Abril 1981

Cumpre ressaltar que (7) e (8) conduzem a resultados que deixam de ser 5. RESULTADOS NUMÉRICOS

verdadeiros quando A e B se aproximam das fronteiras de separação en­ é

Tendo em vista o interesse prático da faixa de ondas médias para os servi­
tre as seções. Isto resulta da utilização do princípio da fase estacionária e

ços de radiodifusão, esta seção apresenta uma série de resultados nu­
’da invalidade do conceito de impedância de superfície na região da fron­

méricos tomando por referência a freqüência de 1 MHz. Outros resulta­
teira (suposta abrupta).

dos para as fixas de HF e LF podem ser encontrados cm Calmon (10).

Neste ponto é interessante introduzir algumas considerações relativas a Para as constantes elétricas do solo foram selecionadas:

efeitos de reflexão e refração observados na fronteira de separação de

dois meios. Quando ondas eletromagnéticas dc superfície se propagam (I) Solo pobre

através da fronteira de separação entre a terra e o mar (linha que define o er = 15 ; a = 10—3 mho/m

litoral) situada obliquamente ao percurso dc propagação, cvidcncia-se

que uma parte da onda incidente é refletida e outras efeitos são notifica­ (II) Solo médio

dos. Wait (7) tratou analiticamente a questão e mostrou que uma onda es­

tacionária pode existir em frente à fronteira, resultante da interferência er = 15; a = 10- 2 mho/m

da onda incidente com a refletida. Verifica-se que esta última depende

criticamente do ângulo dc incidência, de modo que, para incidências in­ (III) Água do mar

feriores a 45" relativamente à normal à fronteira, a onda refletida é des­ 8r = 80; a = 4 mho/m

prezível. Outra característica apresentada pela onda refletida é a rápida

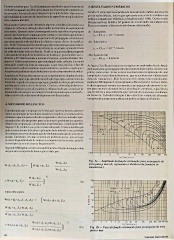
atenuação a partir da linha de separação, o que vem justificar o fato de As figuras 3 a e 3b apresentam as variações cm ampl itude e fase da função

não ter sido levada cm conta nas seções anteriores, quando se supõe que o atenuação para a propagação em um trajeto dc duas seções, da terra (solo

rcccpte pobre) para o mar. Estas curvas mostram uma recuperação do sinal

A análise dc Wait também mostrou um comportamento singular da onda (amplitude e fase) além da fronteira, que se acentua com o afastamento

transmitjda. qual seja, um efeito dc refração logo após o cruzamento da desta do transmissor. Este fenômeno foi comprovado cxpcrimcntul-

fronteira, seguido dc uma recuperação gradual da direção primitiva à m enteporM il!ington(3.8)(am plitudc)ePresseycta!( 11)(fase). O efei­

medida que a onda se afasta da mesma. Com isto. a formulação deste tra­ to de recuperação sempre acompanha a propagação de um meio de me­

balho é válida em casos de incidência oblíqua desde que a condição de nor para um meio de maior índice de refração complexo, o qual deve a

afastamento do receptor em relação à fronteira garanta que a onda refle­ sua existência a uma redistribuiçáo vertical de energia nas vizinhanças

tida c o desvio da onda transmitida possam ser desprezados. da fronteira. Tal redistribuiçáo é inevitável cm virtude das diferentes

variações do campo com a altura em ambos os lados da fronteira.

4. MÉTODO DE MILLINGTON

Considerando que o emprego da formulação rigorosa descrita anterior-

mente na obtenção dc resultados numéricos implica a existência de fa­

cilidades especiais para ocálculo(computador), diversos métodos apro­

ximados têm sido propostos para solucionar o problema cm questão.

Através da comparação com medidas experimentais, o método de Mil­

lington (3,8) cvidcncia-se como o mais adequado. O único detalhe que

podcevcntualmentc dificultara aplicação deste método é a necessidade

dc conhecer as curvas de atenuação do sinal para cada tipo de solo em se­

parado. Entretanto, isto não constitui um problema grave, uma vez que
0 01

já existe disponibilidade dc inúmeros conjuntos destas curvas, para di

versos tipos dc solo c faixas dc frcqüência(9).

Segundo Millington, acxprcssáo analítica para a função atenuação sobre

um percurso composto dc duas seções é dada por

0 001
10 20 50 Hl

D I S T Â N C I A ( k m )

Fig. 3a — Amplitude da função atenuação para propagação da
W ( d , . Z , ) terra para j) mar (dt representa a distância da fronteira ao

W l d i + d i . Z i . Z . ) = [ W ( d | + d i . Z . )

transmissor).

W ( d , , Z . )

V i
W ( d 2, Z 2 )

x W (dI + d2, Z |)
( 9 )

W ( d 2, z . )

TERRA (t 10 ’) PARA

MAR (t - 41 T
e para três seções. f = 1 MHz

160
50

100
50
I I
30
W ( d | + d 2. + d .1, Z l . Z 2, Z . , ) = [ w ( d , + d 2+ d , . Z , ) — 20

-- * 4 — 10

-80
W ( d l + d ; , . Z : ) W ( d l . Z l ) C

x

40
W < d l + d 3. Z , ) W ( d , . Z , )

50
30
20
w l ^ + d : . Z ; ) W ( d , , Z , | V i 1 2 3 5 7 10 D I S T Â N C I A ( k m ) 200 300 500 700 1 u.»
X W ( d , + d 3 + d , . Z | )

( 1 0 ) Fig. 3b — Fase da função atenuação para propagação da terra

w ( d , i + d 2. Z | ) W ( d „ Z . ) para o mar