Page 62 - Telebrasil - Março/Abril 1982

ECONOMICO

Quando analisados através do método da taxa de retorno, estes Um projeto de investimento com vida útil de 4 anos ecom um

fluxos devem ser vistos com muito cuidado, sobretudo porque taxa mínima de atratividade de 4% ao ano.

teoricamente os fluxos não convencionais podem apontar mais

de uma solução para o mesmo problema, isto é, apresentar mais

de uma taxa de retorno.

Isto ocorre porque, matematicamente, a taxa de retorno funcio­

na como o valor que anula o polinómio. Assim, uma alternativa

de investimento não convencional, com seis anos de vida útil e

com três mudanças de sinal, equivale a um polinómio de grau

seis, podendo ter até três raízes reais e positivas, que anulem

este polinómio. Neste caso, trazemos à taxa mínima de atratividade, o fluxo cor­

respondente ao ano 2 para o ano 1.

Teremos então — 2848 x ________ 1 = — 2738,46 que

VaÁ (1 + 0,04)

somando algebricamente com o fluxo correspondente ao ano 1,

vem dar uma formação convencional ao projeto de investi­

mento.

Resolvendo, agora, pelo método da taxa de retorno não corre­

mos mais o risco de encontrar mais de uma taxa que anule este

fluxo de caixa, senão, 3,97%.

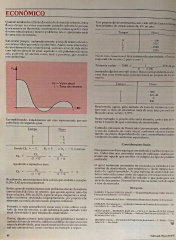
Exemplificando, estudaremos um caso representado por um Neste exemplo o projeto não seria atraente, pois a taxa de re­

polinómio do segundo grau. torno é menor do que a mínima de atratividade.

Tempo Fluxo C ontudo, em casos de fluxos não convencionais, aconselhamos

o uso do método do valor atual; conforme citamos anterior­

mente, ou então, dependendo do caso, aconselhamos também

0 - 1 o método da série uniforme equivalente.

1 5

2 - 5
Considerações finais:

Sendo D0 = - 1, R, = 5 o Dt - - 5, teremos:
Não queremos dizer aqui que um método-é melhor do que o ou­

tro. Todos têm seu momento exato de aplicação. Usamos nor­

D0 + R, malmente aquele que melhor se adapta ao tipo de problema

0 + i Y 0 + i) analisado.

Igualando a equação a zero,
O que é realmente necessário ter em todos os métodos é a taxa

máxima de atratividade, que estabelece o limite mínimo de re­

D,, + ° 2 R| - n torno do capital investido. A taxa mínima de atratividade, tam­

0 + 0’ (1 + 0 bém conhecida como custo do capital, é teoricamente um as­

sunto controvertido, difícil de calcular e que pode gerar uma

Resolvendo, encontraremos dois valores que anulam a equação: série de discussões. Normalmente usa-se como custo do capital

0,38 e 2,62 aproximadamente. a taxa de mercado.

Então, quando equacionamos este problema através do método B ib lio g r a fia

convencional da taxa de retorno, que aponta apenas uma das
G A R M O , E P au l e C A N A D A Jo h n R . — E n g in e e rin g E co n o m y , Collier Macmillan
duas soluções, 38% ou 262%, é provável que cheguemos a resul­ In te rn a tio n a l E d itio n s — 6.*’ E d itio n .

tados incorretos, decidindo, impropriamente, por projetos não

PU C C 1N 1, A b e la rd o d e L im a — M a te m á tic a F in a n ce ira e A n álise d o Investimento
atraentes ou então abandonando projetos rentáveis.

E H R L 1C H , P ie r r e ja c q u e s — A v a lia ç ã o e S e le ç ã o d e P ro je to s d e Investim ento— Edi­
Portanto, o mais aconselhável, neste caso, é não utilizar o mé­ tora A tla s S . A . — S ã o P a u lo .

todo da taxa de retorno, e sim substituí-lo pelo método valor
H E S S , G e ra ld o — M A R Q U E , Jo s é L u iz — P A E S , L .C . R o ch a eP U C C IN I, Abelardo
atual descontado à taxa mínima de atratividade. — E n g e n h a ria E c o n ô m ic a . 9 .- E d iç ã o — E d ito ra D ifel/D ifusão Editorial S.A. — Rio

d e Ja n e iro / S á o P a u lo .

Porém, alguns autores, para superar este problema e manter o
D E F A R O , C lo v is — E le m e n to s d e E n g e n h a ria E co n ô m ica — 3.J Edição — Editora
método da taxa de retorno, utilizam o artifício de usar a taxa mí­ A tla s S .A . — S ã o P a u lo .

nima de atratividade, para transformar um fluxo não convencio­

nal em convencional, como veremos no exemplo a seguir.