Page 34 - Telebrasil - Novembro/Dezembro 1979

Como se pode notar, esta é a etapa das regressões a fim de se obter a for­ A função de regressão utilizada no mo­

alternativas que define toda a consti­ ma analítica mais apropriada para a delo de crescimento do capítulo 3, co­

tuição da função da densidade ideal. função de densidade ideal. mo será visto a seguir, está na faixa in­

termediária do gráfico, com uma
Na segunda etapa estimam-se os parâ­ Após vários exercícios, chegou-se a re­

metros da função, através do critério sultados que indicaram ser a função inclinação, em relação à renda,

de mínimos quadrados. potencial a mais adequada para expri­ próxima de um.

mir a densidade ideal. Dentre todos os 3. O modelo de regressão “cross-sec-

HL Variáveis explicativas
casos analisados, essa função apresen­ tion”

tou o maior nível de correlação para

A princípio, não há restrição quanto qualquer combinação entre amostras e I. Quantificação

ao número de variáveis explicativas variáveis explicativas.

que podem ser inseridas em uma O primeiro problema com respeito à

equação de regressão, embora torne-se Teoricamente, isto significa que a den­ quantificação da densidade telefônica

difícil trabalhar com mais de duas va­ sidade telefônica cresce mais que pro­ satisfatória surge de sua própria defi­

riáveis explicativas, quando não se dis­ porcionalmente à renda p er capita nos nição, em virtude da impossibilidade

põe de suporte material adequado.
países mais pobres, correndo o inverso de se obter indicadores que caracteri­

Por outro lado, não é o número de va­ em países de renda p er capita mais ele­ zem de forma precisa o grau de desen­

riáveis que irá determinar o grau de vada. volvimento de um país.

qualidade da função, mas sim suas ca­ A solução mais simples, em muitos ca­

racterísticas e correlação com a va­ A análise de regressão feita com amos­ sos, é considerar a renda per capita co­

riável dependente. tras de diferentes países, por classes de

renda p er capita, demonstrou esta ten­ mo um indicador aproximado do de­

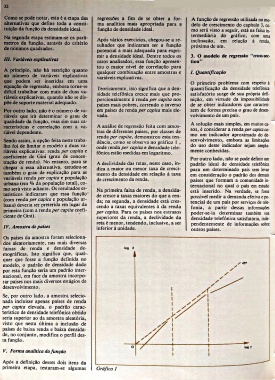
Sendo assim, a opção feita neste traba­ dência, como se observa no gráfico 1 , senvolvimento, embora as limitações

lho foi de limitar o modelo a duas va­ onde renda p er capita e densidade tele­ do uso deste indicador sejam ampla­

riáveis explicativas: renda p er capita e fônica estão medidas em logaritmo. mente conhecidas.

coeficiente de Gini (grau de concen­ Por outro lado, não se pode definir um

tração de renda). No entanto, para se A declividade das retas, neste caso, in­ padrão ideal de densidade telefônica

chegar a essa alternativa, estudou-se dica a maior ou menor taxa de cresci­ para um determinado país sem levar

também o grau de explicação para as mento da densidade em relação à taxa em consideração o padrão dos demais

variáveis renda p er capita e população de crescimento da renda. países que formam a comunidade in­

urbana (em % da população total), co­ ternacional no qual o país em estudo

mo será visto adiante. Os resultados es­ Na primeira faixa de renda, a densida­

tatísticos indicaram que essa função' de cresce a taxas maiores do que a ren­ está inserido. Na verdade, se fosse

(com renda p er capita e população ur­ da; na segunda, a densidade está cres­ possível medir a demanda efetiva e po­

bana) deveria ser preterida em lugar da cendo a taxas equivalentes à da renda tencial de um país por serviços de tele­

primeira (com a renda p er capita coefi­ per capita. Para os países nos estratos fonia, a partir dessas informações
poder-se-ia determinar também sua

ciente de Gini). superiores da renda, a declividade da densidade telefônica satisfatória, inde­

reta é menor, tendendo, inclusive, a ser pendentemente de informações sobre

IV. Amostra de países inferior à unidade. outros países.

Os países da amostra foram seleciona­

dos aleatoriamente, nas mais diversas

faixas de renda e densidade de­

mográficas. Isto significa que, qual­

quer que fosse a função definida no

modelo, o padrão de densidade dado

por esta função seria um padrão inter­

nacional, em face da amostra incorpo­

rar países nos mais diversos estágios de

desenvolvimento.

Se, por outro lado, a amostra selecio­

nada incluísse apenas países de renda

per capita elevada, o padrão carac­

terístico de densidade telefônica obtido

seria superior ao da amostra aleatória,

visto que nesta última a inclusão de

países de baixa renda e baixa densida­

de, no conjunto, modifica o perfil des­

ta função.

V. Forma analítica da função

Após a definição desses dois itens da

primeira etapa, testaram-se algumas