Page 34 - Telebrasil - Janeiro/Fevereiro 1979

cia de erros em número de até

(dmín - 1)/2, em nN posições con­

secutivas. Em diversas situações

práticas, isto é superior até mes­

mo aos mais poderosos códigos

nâo-convolutivos.

13. Conciusões

Foram apresentados os principais

conceitos necessários para mani­

pulação de códigos detectores e

corretores de erros na área da

transmissão digital. Com uma

apresentação exemplificada das

classes de códigos mais comu-

mente empregadas na prática,

compararam-se suas característi­

cas de desempenho.

A classe de códigos BCH tem-se

revelada a de maiores aplicações

no campo das comunicações,

quando se quer aliar um desempe­

nho poderoso na detecção e cor­

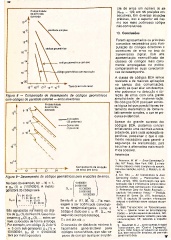
F ig u r a 8 — C o m p a r a ç ã o d e d e s e m p e n h o d e c ó d i g o s g e o m é t r i c o s reção de erros com uma grande

c o m c ó d ig o s d e p a r id a d e s im p le s — e r r o s a le a t ó r io s . simplicidade de implementação.

Os códigos BCH possuem estrutu­

ra lógica tal que possibilita seu tra­

tamento matemático de forma re­

lativamente simples, o que se pro­

curou evidenciar.

Apesar do grande sucesso dos

códigos BCH, podemos concluir

enfatizando uma vez mais a neces­

sidade de, para cada aplicação es­

pecifica, pesquisar o que é real­

mente necessário para garantir a

segurança da transmissão, para

escolher a alternativa mais econô­

mica possível.

Referências

1. Peterson, W. W. — Error-Correcting Co­

des, MIT Press, New York, 1961. É o trata­

mento clássico mais completo do assunto.

Há uma reedição, com E. J. Weldon, Jr., de

1970.

2. Lin, Shu — An Introduction to Error-
F i g u r a 9 - D e s e m p e n h o d e c ó d i g o s g e o m é t r i c o s p a r a e r u p ç õ e s d e e r r o s .

Correcting Codes — Prentice-Hall, Inc.,

New Jersey, 1970. Compilação cuja apre­
No caso do exemplo, k(n - k) = 1, ( 101000001 sentação não é infelizmente sempre clara e

e g» (1) = (11010001). A matriz- 011001000 suficiente, mas com bastante informação.

G a 101000001
geradora do código será 3. Reference Data for Radio Engineers —
011001000
capitulo “ Information Theory” — 5.aedição,

101000001
11 01 00 01 l Howard W. Sams Co. (ITT), Indianapolis,

11 01 00 01 (°) 00 1970. O capítulo 38 contém informações
G

(0) 11 01 00 01 Sendo m = ( 1 1 , 0 0 , 1 0 , . . . 7 ) a men­ amplas e didáticas sobre códigos de pari­
11 01 00 01 sagem a ser codificada convoluti- dade.

l va ou seqüenciaimente, como o 4. IEEE Transactions on Telecommunica­

São agrupados na matriz os dígi­ código é dado por c = m . Goo, no tions — Special Issue on Error-Detecting

tos de goo(1), de N em N. Caso hou­ segundo exemplo teremos. Codes — edição especial de outubro, 1971.

vessem g» (2), g« (3), ..., estes se­ Artigos especialmente voltados para tele­
comunicações: HF, satélites e tropodifu

riam colocados de forma análoga. C = { 1 1 0 , 0 0 1 , 7 0 0 ...) são.

Por exemplo, um código (3, 2) de N O conceito de distância mínima é 5. Gaushell, D. J. - Error Control in Digital

Transmission, em "Control Engineering”,
= 3 com sub-geradores g « (1) = facilmente generalizável para junho, 1972. Artigo introdutório ao assunto

1 0 1 0 0 0 0 0 1 , c j o c ( 2 ) = 0 1 1 0 0 1 0 0 0 códigos convolutivos, que sâo ca­ que, sem entrar em detalhes, dà uma visão

, terá por matriz-geradora pazes de corrigir qualquer seqüên- geral muito boa. atf