Page 40 - Telebrasil - Setembro/Outubro 1977

Neste caso, os pontos de saída ocupam

menos pontos de C do que o total

alcançável por uma coluna completa

do estágio B.

r — 1 K

W ( n ) = I Q ( p ) I P ( u . p )

p = o u = o

o n d e :

P ( u . p )

probabilidade de estarem ocupados os

K-u circuitos de C, acessíveis pelos

circuitos livres de B quando existem u

ocupações nos circuitos de B que tem

acesso a C.

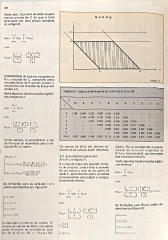
TABELA III - Cálculo de W (n) para N > K < m (N = 10, K = 5, m =20)

Após algumas transformações algébri­

cas chegamos a:

8 1

N — n

W ( n ) = I R ( i , n )

i=o

0 1,000 0,500 0,222 0, 0,023 0,003 -

o n d e : 1 — 0,180 0,200 0,149 0,085 0,035 0,008 — — — —

2 — — 0,027 0,052 0,059 0,049 0,029 0,010 — — ____

3 — — — 0,003 0,009 0,016 0,019 0,017 0,009 — —

R ( i . n )
4 — — — — 0,000 0,001 0,003 0,005 0,007 0,006 —

5 — — — — — 0,000 0,000 0,000 0,000 0,001 0,003

W(n) 1,000 0,680 0,449 0,287 0,176 0,104 0,059 0,032 0,016 0,007 0,003

Como sempre, é aconselhável o uso

de fórmulas de recorrência para o cál­

culo de R(i,n), assim: Os valores de W (n) são obtidos so­ Assim, P(u,p) corresponde à probabi­

mando-se as colunas assim dispostas. lidade de estarem ocupados os

K-f.n-u circuitos de B, que tem acesso

f R ( o , N ) 1 4.3. Acessibilidade plena para aos circuitos livres de C.

N ^ K < m (figura 71.
Após algumas transformações algébri­
( N n - ^ ( K . ) ( r 1 . )
R ( i M . n ) R(i.n) É o caso de rotas com reduzido núme­ cas teremos:
( n + i » 1 K ) ( i + 1 ) ( m i )
ro de circuitos, onde é feita a conexão

de um tronco a mais de um ponto de
(n~K+i) (N-n+1) W ( n ) I R ( u , n )

R í i . n 1 ) R ( i . n ) saída C, aproveitando assim, as saídas
n(N—n+1 -i) u = o

remanescentes para reduzir o conges­

tionamento interno. o n d e :

As limitações para as variáveis i e n

podem ser descritas por (figura 6):

( r_1 ' » n r -1')
r-1 x \ K - f * n - u / \ u / \ n - u / K -f* n -u
R ( u , n ) =
W ( n ) = £ Q ( p ) I P ( u , p ) ¦ n 3

0 < i < K p = o u = o \ K -f-n -u / Vn /

O < i < r 1 o n d e :
As limitações para R(u,n) podem ser

descritas por (figura 8):
O < n < N

( K - f - ’ n - u )
P ( u , p ) - -
' ¦ n + i < N O < u < x
Í

O exemplo numérico da tabela III O < n < N

mostra os valores de R(i,n) calculados

pelas fórmulas de recorrência para O < n - u < N - x

N - 10, K - 5, m = 20, r = 13 e a = 0,6. x K í * n

V O < K - f n - u < r - 1