Page 12 - Telebrasil - Março/Abril 1978
P. 12
t ' ^ H P 1
< -TM
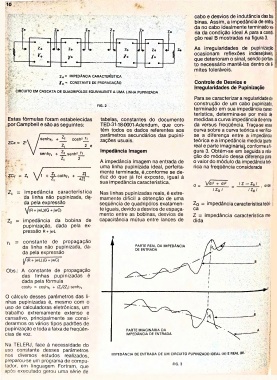
cabo e desvios de indutância das bo
binas. Assim, a impedância de entra-1
da no cabo idealmente terminado va
ria da condição ideal A para a condi-(l
ção real B mostradas na figura 3.
As irregularidades de pupinização
ocasionam reflexões indesejáveis,
que deterioram o sinal, sendo portan
to necessário mantê-las dentro de li
mites toleráveis.
Controle de Desvios e
Irregularidades de Pupinização
Para se caracterizar a regularidade de
construção de um cabo pupinizado,
terminado em sua impedância carac
terística, determina-se por meio de
Estas fórmulas foram estabelecidas tabelas, constantes do documento medidas a curva impedância de entra
por Campbell e são as seguintes: TED-31-18-0001-Adendum, que con da versus freqüência. Traça-se essa
tém todos os dados referentes aos curva sobre a curva teórica e verifica-
*
X y ' #,
-1 . *’
i*V*\*’ parâmetros secundários das pupini- se a diferença entre a impedância
senhy, + ± cosh2 Yx zações usuais. teórica e a impedância medida (parte
Z C 7 T = Z 1
íL. • z, 2 e real e parte imaginária^, conformeafi-
r/::.
Impedância Imagem gura 3. Obtém-se em seguida a rela
* r w » —
r senhy. + Z» senh2 Yl
Z, 2 ção do módulo dessa diferença para
A impedância imagem na entrada de o valor do módulo da impedância teó
* •
B i * «
uma linha pupinizada ideal, perfeita rica na freqüência considerada
mente terminada, é,conforme se de
'¦ z c T = z, 1 + Ä co.h„ + « duz do que já foi exposto, igual à
sua impedância característica. VcJi2 + drJ
> . d = / Z - Zn / onde
/Z n / / Zo /
impedância característica
A Nas linhas pupinizadas reais, é extre
da linha não pupinizada, da mamente difícil a obtenção de uma il
da pela expressão seqüéncia de quadripólos exatamen Zo impedância característica teóri- V
I
(R + jwL)/(G + jwC) te iguais, devido a desvios de espaça ca
mento entre as bobinas, desvios de Z = impedância característica me
z, = impedância da bobina de capacitância mútua entre lances de dida
pupinização, dada pela ex
pressão R+jwL • I
• Ä
constante de propagação
r i
da linha não pupinizada, da PARTE REAL OA IMPEDÂNCIA
DE ENTRADA
da pela expressão
(R+jwL).(G +jwC)
Obs.: A constante de propagação
das linhas pupinizadas é
dada pela fórmula
coshy = coshy, + (Z2/2Z,) senhy,
O cálculo desses parâmetros das li
nhas pupinizadas é, mesmo com o
uso de calculadoras eletrônicas, um
trabalho extremamente extenso e
cansativo, principalmente se consi
derarmos os vários tipos padrões de
pupinização e toda a faixa de freqüên- PARTE IMAGINÁRIA DA
cias de voz. IMPEDÂNCIA DE ENTRADA
Na TELERJ, face à necessidade do
uso constante desses parâmetros
nos diversos estudos realizados, IMPEDÂNCIA DE ENTRADA DE UM CIRCUITO PUPINIZADO IDEAL IA) E REAL (8). iK *
V.
'.7 .‘V
+-S.
’ -I > ¦ •
preparou-se um programa de compu . - I ; •
•
•«5". ,
tador, em linguagem Fortram, que FIG. 3 , • ^ .¦ : • r •
• # * •• • I
.3;
» _
• '
após executado gerou uma série de