Page 20 - Telebrasil - Setembro/Outubro 1976
P. 20
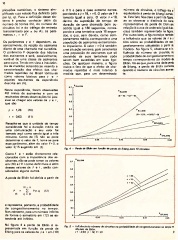
plicações numéricas, o sistema sim e (11) e para o caso extremo corres número de circuitos, o tráfego (ou o 1
plificado cujo estado fica definido pelo pondendo a 0 -1 8 , y * 0. O valor de F é equivalente à perda de Erlang) aumen
par (p, q). Para a definição desse sis tomado igual a zero. 0 valor 0 * 1 8 , ta. Este fato fica claro a partir da figura,
tema ê preciso conhecer além do dentro da suposição de tempo de ao se observar a distância da curva
número de fontes (N), do número de duração de uma chamada bem su representativa da perda de Elldin em
circuitos (n) e do tráfego de entrada cedida igual a 180 segundos, corres relação à curva de ordenada igual à ab-
(caracterizado por a ou A)r os parâ ponde a uma tentativa cada 10 segun cissa também representada na figura.
metros , r e F. dos, o que, sem dúvida, como com Por outro lado, a figura realça também;
portamento médio, corresponde a uma a influência que os valores de 9 e r
Os parâmetros ? e r dependem, es população de assinantes extremamen têm sobre as probabilidades de con
sencialmente, da reação do assinante te impaciente. O valor r * 0 é também gestionamento calculadas a partir do
diante de uma chamada mal sucedida. uma situação extrema, pois caracteriza modelo. Na figura 5, observa-se a in
O parâmetro F depende dos hábitos uma população de assinantes que só fluência do número de circuitos, na
dos assinantes e será, possivelmente, desistirão de suas tentativas após probabilidade de congestionamento no
variável de uma classe de assinantes serem bem sucedidas em suas liga tempo correspondente ao modelo de
para outra. Tendo em vista a inexistên ções. De qualquer maneira, a figura Elldin. Vê-se que, para uma dada perda
cia de medidas sistemáticas visando a realça o fato de que o efeito de cha de Erlang, a perda de Elldin aumenta
caracterização dos efeitos das cha madas repetidas é mais intenso à quando o número de circuitos aumen
madas repetidas no Brasil tomou-se medida que, para um determinado ta.
como valores básicos para 0 e r 1
aqueles resultantes da experiência
descrita em (51.
Nesta experiência, foram observadas
451 linhas de assinantes e com os
resultados destas observações foi pos
sível se chegar aos valores de ;? e r ,
que são
H - 1,26 (10)
r - 0,63 (11)
Ressalte-se que a unidade de tempo
considerada foi a duração média de
uma comunicação e seu valor foi
tomado aqui como sendo igual a trás
minutos. Como d© |5| não se pode
determinar o valor de F, toma se para
esse parâmetro, além do valor F*0, o
valor 0,15 sugerido em (3)
4 - àe lãiàn em fu tu ro <U perde de Bdeng per* 10 circuitos.
Como 0 e r estão dirotomente rela*
cíonados com a impaciência do» as
sinantes, não se pode tomar os valores
em (10) e (11) como definitivo» e além
desses valores de M r , serão con
siderados alguns outros.
A perda de Elldin foi obtida a partir de
N - n
P - Z P(n.q) (12)
ct q - 0
e representa, portanto, a probabilidade
de congestionamento no tempo.
Naturalmente, para um número infinito
de fontes o somatório em (12) se es
tenderia até infinito.
Na figura 4 a perda de Elldin ê re
presentada em função do perda de
Erlang para os valores de e y em (10)